Beginners Guide on How to Memorise Trigonometric Functions?
Trigonometric functions are an essential part of mathematics and play a significant role in various fields, such as physics, engineering, and computer science. Memorising trigonometric functions is essential for students who are studying these subjects. However, memorising them can be challenging, especially for those struggling to remember mathematical formulas and concepts. In this blog post, we will provide you with some tips and tricks on how to memorise trigonometric functions effectively.
- Understand the Basics of Trigonometric Functions
- Use Acronyms to Memorise Trigonometric Functions
- Create Mnemonics to Memorise Trigonometric Functions
- Practice with Trigonometric Tables
- Use Visualisation Techniques
- Practice with Trigonometric Identities
- Apply Trigonometric Functions to Real-World Problems
- Wrapping Up
1 Understand the Basics of Trigonometric Functions
Before you begin to memorise trigonometric functions, it is essential to have a clear understanding of what they are and how they are used. Trigonometric functions are mathematical functions that relate to angles in a right triangle. The three primary trigonometric functions are sine, cosine, and tangent, commonly denoted as sin, cos, and tan, respectively.
The sine function (sin) is the ratio of the opposite side of a right triangle to its hypotenuse. The cosine function (cos) is the ratio of the adjacent side of a right triangle to its hypotenuse. The tangent function (tan) is the ratio of the opposite side of a right triangle to its adjacent side.
2 Use Acronyms to Memorise Trigonometric Functions
One popular method of memorising trigonometric functions is by using acronyms. Acronyms are a set of letters that are used to represent a word or phrase. In this case, we can use acronyms to represent trigonometric functions.
One popular acronym used to represent trigonometric functions is SOH-CAH-TOA. This acronym represents the three primary trigonometric functions in the following order: sine, cosine, and tangent. The acronym can be expanded as follows:
SOH: Sine = Opposite/Hypotenuse
CAH: Cosine = Adjacent/Hypotenuse
TOA: Tangent = Opposite/Adjacent
By using the acronym SOH-CAH-TOA, you can easily remember the three primary trigonometric functions and their respective formulas.
3 Create Mnemonics to Memorise Trigonometric Functions
Another effective method of memorising trigonometric functions is by creating mnemonics. Mnemonics are memory aids that use associations between easy-to-remember information and the information that needs to be remembered.
For example, you can create a mnemonic to remember the sine function as “Sugar Over Honey.” This mnemonic represents the formula for the sine function, which is the ratio of the opposite side of a right triangle to its hypotenuse. By associating the phrase “Sugar Over Honey” with the sine function, you can easily remember the formula for the sine function.
Similarly, you can create mnemonics for the cosine and tangent functions. For example, you can remember the formula for the cosine function as “Carrying Apples Help” and the formula for the tangent function as “Two Old Ants.”
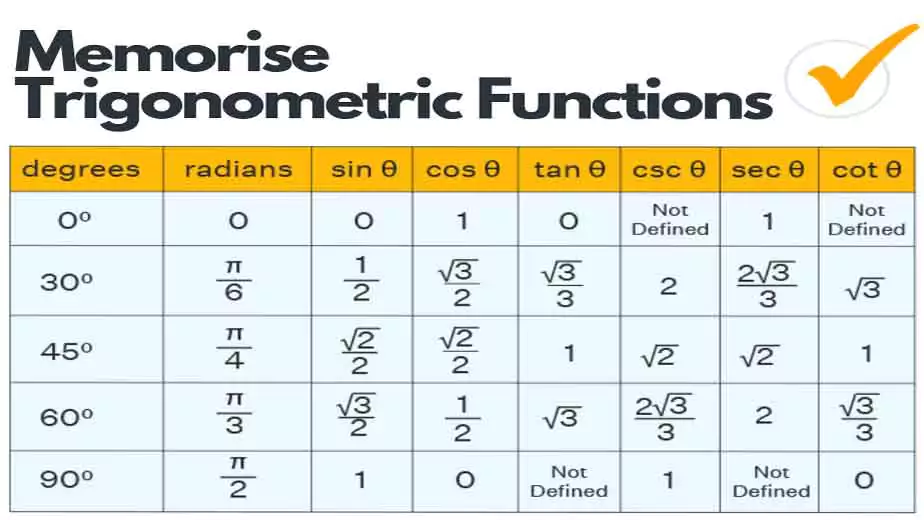
4 Practice with Trigonometric Tables
Trigonometric tables are tables that provide values for the trigonometric functions at different angles. These tables are useful for solving trigonometric equations and for finding the values of the trigonometric functions at specific angles.
By practising trigonometric tables, you can improve your ability to memorise the values of trigonometric functions. You can start by memorising the values of the trigonometric functions at common angles, such as 0, 30, 45, 60, and 90 degrees. Once you have memorised these values, you can move on to memorising the values of the trigonometric functions at other angles.
5 Use Visualisation Techniques
Visualisation techniques can be helpful in memorising trigonometric functions. Visualisation involves creating mental images that help you remember information.
One effective visualisation technique is to imagine a right triangle with specific angles and lengths of the sides. By visualising the triangle, you can associate the angles and lengths of the sides with the trigonometric functions.
For example, if you imagine a right triangle with a 30-degree angle, you can associate the sine function with the opposite side of the triangle, the cosine function with the adjacent side of the triangle, and the tangent function with the ratio of the opposite side to the adjacent side. By using visualisation, you can make connections between the trigonometric functions and their definitions.
6 Practice with Trigonometric Identities
Trigonometric identities are equations that relate the trigonometric functions to each other. By practising with these identities, you can improve your understanding of trigonometric functions and their relationships.
For example, one of the most commonly used trigonometric identities is the Pythagorean identity, which states that sin^2(x) + cos^2(x) = 1. By memorising this identity, you can easily find the value of one trigonometric function given the value of another.
Another useful trigonometric identity is the double-angle identity, which states that sin(2x) = 2sin(x)cos(x) and cos(2x) = cos^2(x) – sin^2(x). By memorising these identities, you can simplify trigonometric equations and expressions.
7 Apply Trigonometric Functions to Real-World Problems
Finally, one of the most effective ways to memorise trigonometric functions is by applying them to real-world problems. By solving real-world problems, you can see the practical applications of trigonometric functions and develop a deeper understanding of them.
For example, you can apply the sine function to determine the height of a building or tree by measuring the angle of elevation and the distance from the building or tree. By using trigonometric functions in practical applications, you can improve your ability to remember them and understand their importance.
8 Wrapping Up
Memorising trigonometric functions can be challenging, but with the right techniques, it can become easier. By understanding the basics of trigonometric functions, using acronyms and mnemonics, practising with trigonometric tables and identities, applying visualisation techniques, and solving real-world problems, you can improve your ability to memorise and apply trigonometric functions in your studies and future career.
You would also love our blog on how to type the Pi symbol: keyboard shortcuts to Unicode. Make sure to check it out!
Community Q&A
About This Article
This article has been viewed 634 times.



